La precisión en los cálculos científicos por computadora

Edscott Wilson García y Guillermo Morales-Luna

Introducción

¿Cuánta gente confía ciegamente en los resultados que arroja una computadora? ¿Qué peligro plantean para la precisión de los cálculos científicos realizados por computadora las velocidades de procesamiento cada vez mayores? En casi todas las ramas de la ciencia, si no es que en todas, se utiliza alguna expresión numérica que involucra cálculos. Aún la más rebuscada ecuación científica, si dispone de solución numérica, se resuelve con operaciones aritméticas fundamentales. Pero como todas las herramientas construidas por el ser humano, la computadora tiene sus limitaciones.

Durante la Guerra del Golfo, el 25 de febrero de 1991, un projectil Scud iraquí hizo blanco en la base militar de Dahrahn en la Arabia Saudita, matando a veintiocho soldados: falló el intento de intercepción del cohete Patriot. Posteriormente se condujo un estudio para determinar las causas de la falla: el sistema de con­trol tenía un contador en incrementos de una décima de segundo. Mediante punto flotante, en la base binaria utilizada por la computadora, 0.1 tiene un patrón fraccionario que se trunca. Consecuentemente, la pre­cisión de 24 bits del sistema Patriot, tenía un error de diez millonésimas de segundo en su contador de tiempo. Al cabo de cuatro días el error se acumuló hasta llegar a un tercio de segundo, lo cual implicó una desviación de 700 metros. Para efecto de intercepción del projectil Scud, un error de 700 kilómetros hubiera producido el mismo resultado final.

En el Centro de Estudios Avanzados del Instituto Politécnico Nacional (Cinvestav) y el Instituto Mexicano del Petróleo (imp), así como en el Lawrence Berkeley National Laboratory en Estados Unidos, y el Institut National de Recherche en Informatique et en Automatique, en Francia, entre otros centros de investigación, se ha trabajado en el problema de la realización de cálculos digitales científicos con precisión certera, es decir, la obtención de resultados en los cuales se puede afirmar con certidumbre hasta qué dígito decimal el resultado es verdadero. Para el laboratorio de cómputo, la precisión certera es análoga a lo que se conoce en química como "cifras significativas", un dato in­dispensable para todos los análisis de laboratorio.

Aunque existen paquetes numéricos como Matemática (Wolfram) y Maple (Maplesoft) con los que se pueden resolver algoritmos con precisión arbitraria o números racionales exactos, su funcionamiento de "caja negra" no permite verificar que las operaciones se hagan de manera correcta, óptima o adecuada al problema en particular. Para el investigador es fundamental tener la capacidad de verificación de los resultados. Por ende, el cómputo científico hoy en día se hace en su mayor parte con los lenguajes FORTRAN y C. El propósito de este artículo es describir cómo puede trabajar un programador científico para lograr mejor pre­cisión utilizando cualquiera de estos lenguajes.

¿Cuál es la precisión?

La precisión computacional está determinada primariamente por la cantidad de dígitos con los que se efectúan las operaciones aritméticas, conocida a partir de la longitud de palabra del procesador. La palabra establece el número entero más grande que se puede representar con exactitud. En el procesador Intel modelo 8088, por ejemplo, se tenía una longitud de ocho bits, que proporcionan un entero máximo de 256. Concatenando dos palabras de este procesador (precisión doble) se pueden obtener cuatro cifras decimales significativas. Como se puede observar en el Cuadro 1, el ta­maño de la palabra, y por ende la precisión, ha ido en constante aumento.

Cuadro  1. Dígitos de precisión decimal para operaciones con números enteros con respecto de la velocidad y tamaño de palabra.

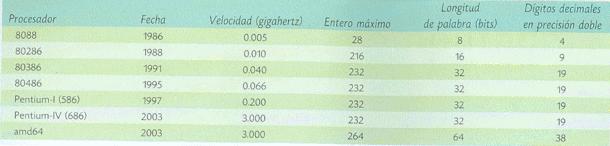
Para un procesador con una longitud de palabra de 32 bits se obtienen 19 dígitos decimales en precisión doble, mientras que para los procesadores de 64 bits -de última generación- se obtienen 38. Generalmente una decena de dígitos decimales es suficiente para la mayoría de los propósitos de cálculo. El advenimiento de la tecnología láser implica que se pueden realizar mediciones sobre objetos del mundo físico con un creciente grado de exactitud. Esta información requiere de mayor precisión en los cálculos computacionales.

Al efectuar cada operación aritmética se reduce, por cuestiones de redondeo y truncamiento, el número de dígitos significativos del resultado final. Cualquier operación aritmética sobre un número x para obtener un resultado y incurre obligatoriamente en un error de redondeo, Exy. Consecuentemente, si el valor x representa una cantidad con una tolerancia ±d, en el resul­tado será de ±E con E = d+ Exy. Muchos algoritmos de cálculo, como los métodos de Newton-Raphson y Runge-Kutta para resolver numéricamente ecuaciones diferenciales que aparecen en los modelos de simulación de plantas y procesos de refinación, son sujetos a una serie repetitiva de operaciones donde los resultados se vuelven a alimentar como datos en cada iteración. ¿Hasta qué punto afectarán estos errores de redondeo el resultado final? Eso no es sencillo de contestar, ya que el cálculo del error supera en complejidad al problema numérico. ¿Qué se puede hacer al res­pecto?

Por un lado se puede adquirir un procesador con tamaño de palabra superior para trabajar con representaciones numéricas de mayor longitud, pero un vistazo al Cuadro 1 es suficiente para constatar que esto es insuficiente. Nótese que la velocidad del reloj de los procesadores ha ido en constante aumento, pero la razón de crecimiento en tamaño de palabra no ha sido equiparable. En menos de veinte años, el hardware de los procesadores multiplicó la velocidad de procesamiento por 600, mientras que la precisión de las operaciones -determinada por el tamaño de palabra-aumentó tan sólo cuatro veces. La parte faltante del aumento de precisión en el hardware debe ser suplida por métodos de software cada vez más complejos. Al aumentar la velocidad de procesamiento también se abrió la posibilidad de aplicar métodos numéricos más sofisticados, con un creciente número de operaciones aritméticas. Ello también aumenta los errores por redondeo.

Un ejemplo donde la precisión juega un factor importante es la exploración petrolera. Para la prospección geofísica se utiliza un modelo matemático basado en inducir ondas sísmicas y analizar los resultados mediante la ecuación de onda. Con esto es posible predecir la forma de las capas de roca bajo la superficie. Pero los datos que se alimentan son cuantiosos, y el núme­ro de operaciones que se tienen que realizar, muy elevado. Suelen pasar días antes de obtener un resultado utilizable. La falta de precisión en mediciones y pérdida de precisión en operaciones aritméticas induce un margen de error, que cuando se aplica a la selección de sitios para la perforación de pozos puede llegar a costar millones de dólares. El aumento en la velocidad de los procesadores ha hecho que el tiempo para obtener los resultados vaya disminuyendo constantemente, pero los resultados no son más exactos.

El error relativo se refiere al error de redondeo que se presenta en cada resultado parcial al efectuar una operación aritmética, y afecta todas las operaciones subsecuentes que utilizan el resultado parcial como operando. Los errores relativos se acumulan, y cada resultado parcial tiene asociado un error relativo total. Algunos métodos para estimar los errores inducidos se encuentran descritos en el trabajo de Miller y Spooner (1975), donde se verifica que el análisis de error eleva al cuadrado la complejidad del algoritmo numérico. Por dicho motivo, en la práctica el análisis de error nunca se lleva a cabo.

Entonces, ¿qué se puede hacer en cualquier rama científica donde hay necesidad de exactitud en los cálculos para garantizar que los resultados tengan la precisión requerida y no son simplemente iteraciones sobre errores de redondeo?

Las metodologías para acotar el error incluyen la precisión arbitraria (donde se extiende hasta el límite de la máquina la memoria utilizada para almacenar los dígitos), los números racionales (donde en lugar de utilizar un punto flotante se almacenan dos números enteros para representar el cociente, p/q), la aritméti­ca de intervalos (donde se va modificando un intervalo de confianza), y la aritmética de rangos (donde el intervalo de confianza determina de manera dinámica a la precisión arbitraria).

El lenguaje
Cuando el investigador busca precisión en los cálculos, deberá cambiar la aritmética con la que se efectúan las operaciones escogiendo el método que más convenga. La utilización de cualquier méto­do para incrementar la precisión implica un aumento en la cantidad de operaciones que se efectúan en el procesador. Por tanto, es imperativo escoger el lengua­je de programación idóneo. Una de las desventajas del FORTRAN es que permite la programación no estructurada, la cual tiende a producir código ejecutable menos eficiente. Por ello, el programador que utilice este lenguaje deberá poner especial cuidado en utilizar la sintaxis estructurada. Para el programador en C este detalle no es tan importante, ya que el lenguaje mismo es estructurado. Sin embargo es importante que se considere el uso de FORTRAN cuando se cumplen las dos siguientes condiciones:

El investigador dispone de un compilador de FORTRAN-95 optimizado para la arquitectura del hardware (por ejemplo, Lahey/Fujitsu para Windows/ Linux/ Solaris).

El algoritmo de cálculo involucra aritmética vectorial/matricial y los resultados de la aritmética matricial en precisión doble no acarrea un error que pudiese ser significativo (es decir, algoritmos con ciclos de iteración breves).

Cuando se cumplen estas dos condiciones, entonces es aconsejable la utilización de FORTRAN-95 para aprovechar las funciones MATMUL, TRANSPOSE, PRODUCT, SUM, MAXVAL y otras que generan código binario optimizado. Cuando se trabaja únicamente con aritmética escalar, es posible generar binarios más eficientes con C, y la selección del lenguaje se convierte en una preferencia del programador. Los programadores científicos de instituciones como el National Center for Supercomputing Applications (NCSA), el Los Alamos National Laboratory (LANL), y el Argonne National Laboratory (anl), por citar unos cuantos ejemplos estadounidenses, han obtenido buenos resultados combinando los dos lenguajes, ya que las instrucciones de FORTRAN-95 y C++ se pueden enlazar en el programa ejecutable final. Una vez definido el lenguaje, resta determinar la metodología. Es aconsejable para el programador científico no partir de cero, sino aprovechar el código ya escrito y comprobado que puede incorporar directamente en sus programas, o conjuntar en el paso de enlazamiento del código máquina.

Lo arbitrario
La precisión arbitraria es una extensión del formato IEEE de punto flotante que permite almacenar una cantidad variable de dígitos. Esta modalidad se limita únicamente por la capacidad de memoria de la computadora. Los números de precisión arbitraria se expresan mediante un vector de palabras, donde cada elemento representa una porción de dígitos de la mantisa, expresado en términos de una base numérica. La base utilizada es la que más convenga de acuerdo a la arquitectura del procesador; comúnmente, el máximo entero mostrado en el Cuadro 1. Por ejemplo, en una computadora de 32 bits la base sería B=2³². Algunas computadoras son capaces de efectuar operaciones aritméticas de punto flotante con más velocidad, y hay quien prefiere utilizar una base expresada en tér­minos de un número de tipo punto flotante.

En la aritmética se aplican los métodos clásicos. Pero cuando los números de precisión múltiple rebasan varios miles de dígitos, se puede lograr una aceleración en la multiplicación aplicando el método de Karatsuba, o bien haciendo una conversión a aritmética modular y aplicando transformadas rápidas de Fourier. Estas dos técnicas están descritas en el texto clásico de Knuth (1981).

Al efectuar una multiplicación de dos números de n dígitos, el producto que se obtiene consta de 2n dígi­tos, de los cuales se desecharán n. Es posible acelerar el proceso de multiplicación si los dígitos sobrantes no se incluyen dentro del algoritmo de multiplicación desde un principio. Sin embargo, no es conveniente desecharlos todos, ya que esto implicaría un mayor error en el redondeo final. Los dígitos a partir del n+1, conservados para el proceso de multiplicación -y que se desecharán después del redondeo final-, se llaman dígitos de guardia.

Existe una larga trayectoria en el desarrollo de código de este tipo del cual puede hacer uso el investigador en sus programas. Comienza con el trabajo MP (Multiple Precision) de Brent (1978). MP fue el primero que era independiente de la arquitectura del procesador y que contaba con rutinas para funciones especiales (ln, exp, sin) y constantes irracionales. Funciona con un vector de enteros de precisión sencilla. Entre las fun­ciones de MP encontramos la conversión de valores enteros, reales y doble precisión a formatos MP y viceversa; operaciones aritméticas fundamentales, la elevación de potencias y cálculo de raíces. El código está escrito en FORTRAN, y en la Universidad de California, Bailey (1995) hizo la conversión a FORTRAN-90 con lo cual se permite implementar el código de una manera más natural. Y en el 2002 construye la interfase C++ para mejorar los algoritmos y desempeños, rebautizándolo con el nombre de ARPREC. Para el programador científico, el código fuente de ARPREC es de acceso libre en el sitio http://crd.lbl.gov/~dhbai-ley/mpdist/ para su inclusión en programas de cómputo de investigación en FORTRAN-95 o C++.

ARPREC representa un esfuerzo norteamericano por facilitar los cálculos digitales con precisión. Por otro lado tenemos GMP, que representa un esfuerzo europeo. Este código está disponible en http://www.swox.com/gmp/ .La meta de GMP es la de proporcionar el código con mayor velocidad de ejecución y mejor desempeño. Para ello se vale de código especial para los distintos tipos de procesadores. Su utilización en programas de cómputo de investigación es libre, así como su utilización en proyectos comerciales.

GMP es sustancialmente más rápido que ARPREC, tiene implementada la aritmética racional y existe código compatible para realizar aritmética de intervalos. Su interfase es de C y FORTRAN-77. ARPREC, por otro lado, es compatible a C++ y FORTRAN-95 y dispone de todas las funciones vectoriales y matriciales intrínsecas que lo hace una poderosa herramienta. No es difícil construir un ejecutable que haga uso de ambas bibliotecas de manera simultánea, si el algoritmo así lo requiere.

Lo racional
Los números racionales son aquellos que se pueden expresar como el cociente de dos números enteros, p/q. Para la codificación de estos números, se almacenan dos variables enteras de precisión arbitraria por cada número. Después de cada operación aritmética, se reducen estos enteros con su mayor común divisor para evitar que crezcan de manera innecesaria. Los enteros p y q se manejan de manera exacta. En el momento en que la memoria de la computadora sea insuficiente para expresar a p o q con todos sus dígitos, el cálculo se detiene con un mensaje de error. Por tanto, si el programador científico desea exactitud, la aritmética racional es una buena opción. Pero si sólo desea tener certeza de la preci­sión, puede optar por una metodología de aritmética de intervalos.

Los intervalos
Con la aritmética de intervalos cada número real se aproxima por dos números con representación digital exacta, y la aritmética se efectúa sobre estas parejas. El primero representa una cota inferior y el segundo una cota superior.

La aritmética de intervalos es importante por las siguientes razones:

• Puede ser utilizada para realizar cálculos digitales con cotas garantizadas sobre los errores de todas las fuentes.

• Puede ser utilizada para resolver problemas no lineales, como la solución a sistemas de ecuaciones no lineales y la programación no lineal.

Existen varios esfuerzos por codificar subprogramas de cómputo para la aritmética de intervalos. Uno de los más completos, escrito por Yohe (1979), incluye todas las funciones propias del FORTRAN ANSI. Sin embargo, el número máximo de dígitos en que pueden ser representados los intervalos está limitado por el tamaño de las variables de tipo REAL, lo que en una arquitectura de 32 bits y representación IEEE-S754 significa un intervalo de operación entre ±10^-4485 y  ±10^38.53.

También existe el trabajo de Jansen y Weidner (1986), quienes introdujeron el software ACRITH, diseñado en FORTRAN-77, y que cuenta con subrutinas para la inversión de matrices, cálculo de valores propios y cálculo de la raíz de un polinomio. Los métodos de redondeo utilizados son el redondeo hacia arriba, hacia abajo, más cercano y a cero. Las desventajas son que no puede combinarse con otros subprogramas para el manejo de precisión múltiple. Además, la parte medular del código está escrito en ensamblador para una arquitectura IBM/370, la cual es obsoleta.

El código INTLIB, publicado por Kearfott (1994), está escrito en FORTRAN-77 y su diseño está acorde a la filosofía de los subprogramas de álgebra lineal de código abierto BLAS (Basic Linear Algebra Subprograms), lo cual le permite su utilización conjunta: una poderosa opción. Desafortunadamente, su precisión queda reducida a la aritmética de punto flotante de doble precisión. Como punto favorable está su interfase FORTRAN-90, que permite definir las variables de manera intrínseca y sobrecargar las funciones aritméticas a los operadores convencionales.

Los rangos

La aritmética de rangos conjunta las técnicas anteriores combinando la aritmética de intervalos con la precisión múltiple. De esta manera se maneja en memoria únicamente la precisión que el intervalo requiere, haciendo más eficiente el procesamiento y optimizando los recursos de cómputo.

Jones (1984) propuso un sistema para hacer aritmética de rangos. En su propuesta utiliza un formato de precisión múltiple para evitar los errores por truncamiento. Se almacenan valores para definir el límite superior e inferior de precisión, manteniendo restringida la precisión de la amplitud del intervalo. Definiendo una regla de significancia, basada en la preservación de la precisión sobre la amplitud del intervalo, se eliminan los dígitos no significativos después de cada operación, acotando así el crecimiento en el número de cifras conforme avanza el cálculo. Mediante las re­glas de significancia, Jones demostró que con un núme­ro modesto de dígitos de guardia se puede garantizar una tasa baja de pérdida de precisión. Y aunque los resultados expuestos por Jones son significativos y prometedores, no existe desde su publicación un esfuerzo por codificar las rutinas que hiciera uso de las reglas de significancia.

El esfuerzo más cercano está en el trabajo de Aberth y Schaefer (1992). Codificaron una biblioteca en C++ para la aritmética de rangos, pero que carece de las reglas de significancia necesarias para evitar la pérdida de precisión. Por ejemplo, se guarda el valor del intervalo como un solo número, lo cual es un error.

Para el programador científico que se interesara por la utilización de rangos, sería conveniente revisar el código de Aberth y Schaefer para introducirle las reglas de significancia de Jones.

En fechas recientes se ha notado un renacimiento en la utilización de aritmética de rangos. Este interés se debe en parte a la mejora sustancial en poder de procesamiento y la creciente necesidad de cálculos más precisos. Por ejemplo, para sistemas de procesamiento de señales de punto flotante realizado en el 2003 por Fang y colaboradores (2003), o el dimensionamiento de circuitos analógicos por Lemke y colaboradores (2002).

Conclusiones

En algunos casos quizá no sea necesario aplicar uno de los métodos descritos con anterioridad. Puede ser suficiente pensar en binario, lo cual no es difícil. Sólo hay que recordar el sistema inglés de medición: la pulgada no se divide en décimas, sino que se divide en fracciones, todas potencias de 2, tales como 1/2, 1/4, 1/8, 1/16, 1/32, 1/64. Al dividir un intervalo o un área, o asignar valores para un incremento, esta forma de fraccionar la unidad es digitalmente más exacta que la división decimal.

Los programas que extienden la precisión requieren de mayor tiempo de cómputo. Pero el avance en la velocidad de procesamiento y las posibilidades de realizar cómputo en paralelo auguran que su utilización en el futuro será cada vez mayor. Para estar a la vanguardia en el desarrollo de programas de cómputo hay que saber cómo extender la precisión y fiabilidad de los resultados computacionales.

Hay gran cantidad de líneas de código fuente ya escritas que el investigador puede usar para desarrollar sus propios programas, y así dedicar sus esfuerzos a esa característica o idea única que marca el trabajo como propio. Cuando se quiere ver más lejos conviene, como hizo Newton, pararse sobre los hombros de gigantes.

Bibliografía

Aberth, O., y M. J. Schaefer (1992), "Precise Computation Using Range Arithmetic, via C++", ACM Trans. Math. Soft., 18, 481-491.

Bailey, D. H. (1995), "A FORTRAN-90 Based Multiprecision System", ACM Trans. Math. Soft., 21, 379-387.

Brent, R. P. (1978), "A FORTRAN Multiple-Precision Arithmetic Package", ACM Trans. Math. Soft., 4, 57-70.

Fang, C. F., T. Chen y R. A. Rutenbar (2003), "Floating­point Error Analysis Based on Affine Arithmetic", http://amp.ece.cmu.edu/Publication/Fang/icassp2003-fang.pdf.

Jansen, P., y Weidner P. (1978), "High Accuracy arithme­tic Software —Some Tests of the ACRITH Problem-Solving Routines", ACM Trans. Math. Soft., 12, 62-70.

Jones, C. B. (1984), "A Significance Rule for Multiple-Precision Arithmetic", ACM Trans. Math. Soft., 10, 97-107.

Kearfott, R. B., M. Dawnde, K. Du y C. Hu (1978), "Algorithm 737: INTLIB: A Portable FORTRAN-77 Interval Standard-Function Library", ACM Trans. Math. Soft., 20, 447-459.

Knuth, D. E. (1981), The Art of Computer Programming, Vol.2: Seminumerical Algorithms, segunda edición, Addisson-Wesley.

Lemke, A., y L. Hedrich, y E. Barke (2002), "Analog Circuit Sizing Based on Formal Methods Using Affine Arithmetic", http://www.sigda.org/Archives/Proceedings Archives/llcad/llcad2002/07c\_1.pdf.

Smith, D. A. (1991), "Algorithm 693: A FORTRAN Package for Floating Point Multiple-Precision Arith­metic", ACM Trans. Math. Soft., 17, 273-283.

Smith, D. A. (1998), "Algorithm 786: Multiple-Precision Complex Arithmetic and Functions", ACM Trans. Math. Soft., 24, 358-367.

Miller, W. (1975), "Software for Roundoff Analysis", ACM Trans. Math. Soft., 1, 108-128.

Yohe, J. M. (1979), "Software for Interval Arithmetic: A Reasonably Portable Package", ACM Trans. Math. Soft., 5, 50-63.