La codificación de los quipus incas
Hugo Cabrera Ibarra, Haret C. Rosu Barbus, Luis A. Torres González, J. Pablo Treviño Gutiérrez
![]()
Introducción
Aproximadamente en el periodo de 1400 a 1532, el pueblo inca registraba datos importantes de una manera peculiar: haciendo uso de cordeles de algodón u, ocasionalmente, de fibras de animales como la llama o vicuña. Estos objetos, que poseían nudos de diferentes formas y colores, estaban sujetos a una cuerda principal, y toda esta estructura textil se conocía como quipu.
A diferencia de los pueblos mesoamericanos, donde se tienen documentos históricos en forma de códices, en la zona andina son los quipus, las telas que envolvían a las momias, las que se colgaban en los edificios de importancia, las ropas de los jefes, la cerámica y ciertos pequeños frijoles los que contienen la información socioeconómica, así como los conocimientos, tradiciones y relatos religiosos. Los quipus, además, registran fechas y acontecimientos sobresalientes, que no debían olvidarse.
El registro de datos era numérico y se cree que también literario. El primer código ha sido descifrado; sin embargo, el segundo permanece como un enigma, pues los incas no contaban con un sistema de escritura. Se sabe que en Cuzco se tenían datos exactos acerca de la cantidad de personas, sus edades y sexo en las diferentes provincias; a partir de esta observación se pudo apreciar una de las utilidades de los quipus como dispositivos de conteo. Todo indica también que a partir de los quipus los incas conocían el sistema decimal gracias al sistema de nudos, sus colores y sus tamaños.
Un poco de historia
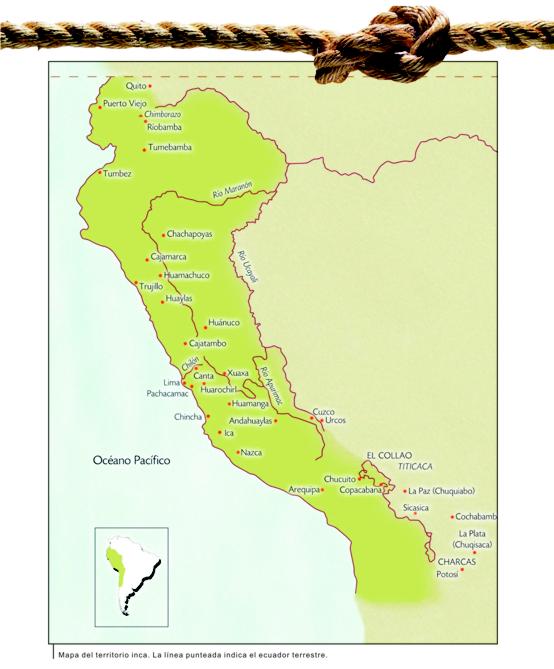
El imperio inca se extendió desde el Ecuador hasta la región central de Chile (véase mapa). El corazón del imperio estaba en Cuzco, en la zona andina del sur de Perú. Hacia 1532 la guerra entre dos hermanos y enemigos alcanzaba su máximo: los hijos de Huayna Capac, Atahualpa, instalado en Quito, y Huáscar, en Cuzco, se disputaban las tierras que su padre había dividido al momento de morir. Esta discordia entre hermanos precipitó la división del imperio inca y la caída de su civilización. Durante ese mismo año, el español Francisco Pizarro desembarcó en la ribera del Ecuador, con planes de conquista. Esto intensificó la debilidad del imperio inca, aunque el final de la conquista no se dio sino después de años de guerra con el último hijo de Huayna Capac, de nombre Manco Capac.
Varios años después, el historiador mestizo Garcilaso Inca de la Vega, conocido también como "El Inca", quien dominaba el idioma quechua local por ser uno de los primeros mestizos, viajó a lo largo del imperio con el fin de registrar por escrito las costumbres y tradiciones del territorio inca. El famoso cronista, nacido en Cuzco, era hijo natural del conquistador español Sebastián Garcilaso de la Vega y Vargas y de la "ñusta" (princesa, en quechua) inca Isabel Chimpo Ocllo. En la primera parte de su obra máxima, los Comentarios reales (1609), De la Vega trata la historia, cultura e instituciones sociales del imperio inca; en tanto que en la segunda, titulada Historia general del Perú (publicada póstumamente en 1617), se ocupa de la conquista de esas tierras y de las guerras civiles. Según la descripción de De la Vega, cuando los indígenas iban a Cuzco a pagar los tributos a los nuevos jefes llegados de Europa, traían una serie de cordeles de diferentes colores sobre los cuales escribían números con la ayuda de distintos nudos. Los cordeles eran ordenados, amarrados y suspendidos a lo largo de una cuerda principal (véase fotografía). Éste es el primer escrito que menciona a los quipus.
 .
.
Los quipus: ¿solo para contabilizar?
La palabra quipu significa "nudo" en quechua. Además del contenido numérico, se piensa que los quipus también tenían información literaria que aún permanece en espera de ser descifrada por el trabajo de investigación de los expertos. Algunos documentos coloniales indican que los quipus eran utilizados para archivar y contabilizar registros, así como para remitir información y mensajes por medio de correos (llamados chasques) a lo largo y ancho del imperio. 
A pesar de que en el imperio inca no se conocía ningún tipo de escritura convencional, su organización era catalogada de una manera detallada y metódica. ¿Será que los quipus también sirvieron para indicar una forma de escritura aún no entendida? Los quipus eran el único modo preciso de transportar información que tenía el pueblo inca: censos, situación de las reservas de producción agrícola, cantidad de productos de la minería, el número de trabajadores, etcétera. En otras palabras, estos dispositivos mantenían la información de los datos históricos, tratados de leyes, documentos de paz o guerra y demás. Los quipus, teniendo esta información, eran transportados por una red de rutas terrestres establecidas por mensajeros organizados en regiones y puntos específicos de todo el territorio imperial.
En esa época, solamente los quipucamayocos (guardianes del quipu) o administradores sabían el significado de los quipus. La mayoría de los quipus en Cuzco o en la provincia fueron destruidos por el ejército de Atahualpa, y más tarde por los oficiales del rey de España, obedeciendo la orden del virrey Francisco de Toledo, con el fin de eliminar la riqueza cultural del imperio inca. Los pocos ejemplares que se pueden admirar hoy en día en museos (alrededor de 600) fueron descubiertos en sitios funerarios, pues era costumbre de los incas sepultar a sus muertos junto con los objetos que utilizaron a lo largo de la vida.

Fotografía de un quipu.
Anatomía de un quipu ¿Cómo se codificaba la información numérica en un quipu? De la Vega es muy preciso en sus observaciones: un quipu está constituido por una cuerda gruesa llamada "principal", sobre la cual se amarran otras cuerdas pequeñas o cordeles de 20 a 50 centímetros de longitud. En un quipu puede haber hasta 2 mil cordeles. Al colocar un quipu sobre un plano horizontal (Figura 1) los cordeles tienen diferente orientación, algunos hacia arriba y otros hacia abajo. La mayoría de los cordeles presentan nudos; pero, ¿qué significan éstos? A pesar de los esfuerzos de los escritores españoles, el misterio de los quipus no podía comprenderse. No fue sino hasta 1912 que el norteamericano Leland Locke fue capaz de descifrar un quipu que se encontraba en el museo de historia natural de Nueva York (Figura 1).
 |
|
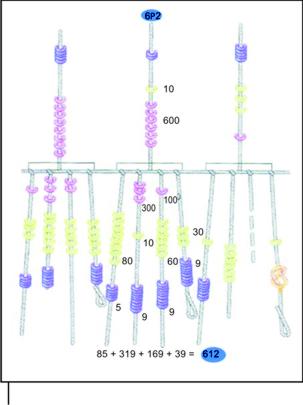
Figura 1. Dibujo de un quipu donde se representa la manera de codificar operaciones de suma. |
Locke usó las descripciones de De la Vega, donde se especificaba que los números codificados por los nudos dependían de la posición en la cual se encontraban sobre cada uno de los cordeles. Los cordeles de un quipu presentan tres grupos de nudos: un grupo inferior, que Locke interpretó como las unidades; un grupo central para las decenas, y un grupo cercano a la cuerda principal para las centenas. Esta hipótesis se confirmó cuando él notó que cada grupo de cordeles de abajo estaba enlazado por una cuerda de arriba cuyo valor, indicado por sus nudos, correspondía a la suma de los otros (Figura 1).
Tres tipos de nudos
De las interpretaciones de Locke se concluye que la codificación de los quipus es similar a nuestro sistema decimal (en base 10). Recordemos las principales características de este sistema: se dispone de 10 símbolos distintos, las cifras del 0 al 9. En un número como el 6139, cada cifra corresponde a la cantidad de una potencia n-ésima de 10, donde n varía desde 0 a la derecha, aumentando una unidad cada vez que se desplaza una posición hacia la izquierda. Por ejemplo, 6 139 = 6 x 103 + 1 x 102 + 3 x 101 + 9 x 10°, o bien, 6 139 = 6000 + 100 + 30 + 9. Nótese que el sistema posicional no está conectado con la base 10. Por ejemplo, los mayas contaban usando un sistema vigesimal, o sea con base 20, usando también un sistema posicional. En el caso de los quipus, las posiciones se consideran con respecto a la cuerda principal, siendo la posición más lejana la de potencia más baja. Por otro lado, los nudos sobre los cordeles son sólo de tres tipos diferentes, a diferencia de las diez cifras actuales (véase Figura 2). Los nudos simples corresponden a las potencias de 10, en los nudos largos un nudo simple en el cual se hacen varios enrollamientos antes de cerrarlo: en (a), cada vuelta es una unidad, b=2, c=5, d=8, y los nudos en forma de 8, que representa una sola unidad. Sobre un cordel los nudos se reparten en grupos de 1 a 9 nudos, así que están las nueve cifras excepto el 0. Cada grupo está afectado de una potencia de 10, que se incrementa al acercarse a la cuerda principal, excepto los grupos de las unidades, que son los únicos grupos de nudos largos y en donde se termina cada número. Sin embargo, cuando hay una sola unidad, el nudo largo de un solo enrollamiento se reduce a un nudo simple y se puede confundir con una potencia de 10. La manera de salir de esta situación ambigua provocada por las unidades aisladas fue, para los incas, hacer un nudo en forma de 8 para una sola unidad. Recuperando el ejemplo del número 6 139, se describe cómo sería su representación quipu: 6 139 = un grupo de 6 nudos simples, pegado a la cuerda principal; un nudo simple, un grupo de 3 nudos simples, un nudo largo de 9 enrollamientos.
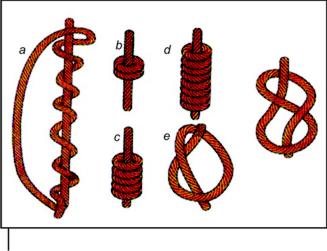
Figura 2. Se muestran los tres tipos de nudos: largos (a partir de dos enrollamientos hasta nueve, a-d, en donde a es un nudo largo no apretado), simples (de potencias de 10, e), y en forma de ocho (para una sola unidad aislada, f).
Sobre las cuerdas, el 0 está indicado por la ausencia de nudo en un grupo. Las unidades son identificadas fácilmente por el tipo de nudo, mientras que los grupos de nudos están alineados en la misma posición sobre todas las cuerdas, de modo que se identifican con facilidad las posiciones sin nudos. Aún más: la falta de ambigüedad para las unidades que se agregan se puede observar en algunos casos, cuando se presentan varios números sobre la misma cuerda.

El desciframiento que hemos comentado se limita al aspecto numérico, y hasta ahora no ha sido contradictorio. En cambio, ¿qué se puede decir de la expresión de las ideas y de los hechos? En este asunto existe mucha polémica. De nuevo hay indicaciones en primera línea del mismo historiador De la Vega. Según él, se puede saber el significado extranumérico de los cordones a través de los colores que llevan. Hay cordones de un solo color, otros de dos, tres y más. Los colores simples y muchas de las combinaciones de los mismos tendrían su propio significado.
Hacia la interpretación del contenido extranumérico
Sobre algunos quipus también se pudo explicar la expresión de los recursos de armas de un pueblo: por ejemplo, las combinaciones de color de manera jerárquica, para las armas; sobre el primer cordel están las armas más nobles, como lanzas, dardos, arcos, flechas, hachas, escudos, etcétera.
El sentido de torsión de los hilos de las cuerdas podría tener también un significado. Vueltas hacia la derecha representan cosas positivas, y al contrario podrían tener un sentido negativo. Tal significado escondido en la torsión de los hilos daría solución al misterio de la ausencia de escritura. ¿Cómo era posible que una civilización con bastante complejidad y organización sobre un territorio tan extenso como casi la mitad de Sudamérica pudiera mantenerse sin escritura?
Gary Urton (2003), reconocido antropólogo de la Universidad de Harvard, ha propuesto la existencia de un código binario en los cordeles de quipu equivalente a una escritura. Se trata de un sistema completamente inédito, que todavía es objeto de debate, y radicalmente diferente de nuestro sistema de escritura. Según Urton, el significado de cada uno de los nudos sería obtenido de un conjunto de cuestionamientos, conocidos también como cadena operacional. ¿El nudo está hecho de lana del camélido denominado llama? ¿Una cuerda está arriba o abajo? ¿Los hilos son rojos o azules?
Por ejemplo, en lo que se refiere a los colores, Urton utilizó la simbología de colores que aún es usada por los tejedores bolivianos, quienes pueden distinguir 24 colores. En total, el antropólogo distinguió seis decisiones binarias y una elección múltiple (el color). Al final, el repertorio de un quipu tendrá un total de 26 x 24 = 1 536 signos de información distintos. Este repertorio es por tanto más amplio que el que posee la escritura cuneiforme de Mesopotamia, y también que el de los jeroglíficos egipcios.
 Urton ha presentado de manera informática todos los detalles de los quipus, de forma que los datos referidos a la codificación estén disponibles al público. En junio de 2003 Carrie Brezine, sastre y matemática, aportó una copia de los quipus encontrados en una caverna situada cerca del lago de los Cóndores, en el norte de Perú. Sobre tres de estos quipus se notaban largas series de nudos casi idénticos, mostrando que la información estaba copiada de unos a otros de la misma manera que los monjes copistas del medievo reproducían los manuscritos a mano.
Urton ha presentado de manera informática todos los detalles de los quipus, de forma que los datos referidos a la codificación estén disponibles al público. En junio de 2003 Carrie Brezine, sastre y matemática, aportó una copia de los quipus encontrados en una caverna situada cerca del lago de los Cóndores, en el norte de Perú. Sobre tres de estos quipus se notaban largas series de nudos casi idénticos, mostrando que la información estaba copiada de unos a otros de la misma manera que los monjes copistas del medievo reproducían los manuscritos a mano.
El contenido extranumérico de los quipus llamó la atención hace una década a través de la investigadora Laura Laurencich Minelli, de la Universidad de Bolonia. Esta investigadora anunció la existencia de un manuscrito titulado Historia et rudimenta linguae piruanorum, del siglo XVII, aparentemente perteneciente a los jesuitas Joan Antonio Cumis y Joan Anello Oliva, y que contiene información detallada sobre los quipus literarios. El documento incluye tres páginas de dibujos firmados por el jesuita mestizo Blas Valera, así como un sobre que contiene un fragmento de quipu.
Según el controvertido documento, algunos quipus, nombrados "reales", se diferenciaban de los que se usaban como registros por tener codificadas sílabas de algunas palabras en quechua. Sin embargo, no existen reglas bien establecidas, como en el caso de los números. De todos modos, parece que las palabras están determinadas por la combinación de la forma de los nudos, sus posiciones y colores.
Más acerca de la codificación de un lenguaje
El grado de complejidad de un lenguaje se puede relacionar con la "cantidad de cosas" que abarca un solo símbolo. Se sabe que el lenguaje es una convención entre un grupo de individuos para asignar una relación entre un símbolo y un objeto o idea. La convención del lenguaje puede entenderse como un código y, a reserva de lo que los expertos en semiótica opinen, puede relacionarse la complejidad de un lenguaje con el grado de complejidad de una comunidad, pueblo o civilización.
Se puede entonces argumentar que la escritura ideográfica es menos evolucionada, pues un solo símbolo representa varias ideas, mientras que en los idiomas occidentales cada palabra está definida de manera unívoca, salvo excepciones. Un pictograma es una imagen simple que representa una idea completa; por ejemplo, "aquí está el baño" o "no pase por aquí”. El ideograma representa una palabra, esto es, un conjunto de fonemas con un significado. Es decir, es más específico que un pictograma y, por tanto, dentro de nuestra argumentación, más complejo. Más allá de las palabras, a las letras les corresponde un sonido específico y único y se requiere un número finito de símbolos para representar una palabra. En este sentido, este tipo de lenguaje (el escrito) sería el más complejo de los tres mencionados.
En el mundo de las computadoras, una letra se representa por un conjunto de números, y más allá de posiciones numéricas, como en el código binario. Puede decirse entonces que, según la propuesta anterior, el lenguaje de las computadoras es más complejo que los idiomas occidentales, al requerir una cierta cantidad de símbolos para representar una sola letra o número. La cantidad de símbolos disponibles y las reglas de combinación entre símbolos juegan un papel importante en la complejidad de un lenguaje.

Esta idea puede servir para establecer una dirección de evolución para el lenguaje, diciendo que es más evolucionado cuanto más especializado está, en el sentido de cuántas cosas representa un carácter (el ideográfico, en que un signo representa varias palabras; binario, en que un signo representa una parte o fracción de una palabra). Cabe especular entonces acerca del grado de evolución del lenguaje escrito de los incas, puesto que se cree, como se ha mencionado antes, que el quechua era sólo el idioma hablado, mientras que el manejo abstracto de los quipus estaba confinado a unos cuantos. Los incas tenían la posibilidad de imprimir, en un simple nudo, varias dimensiones de un código, a saber: la posición, la complejidad y la dirección del nudo y el color del mismo. Así, podría pensarse que un solo nudo es un símbolo individual que abarca varios significados, pero también puede pensarse que un nudo es una manera de almacenar tres o más caracteres o posiciones de código; es decir, que un color representa una regla condicional y que diferentes colores representan números o fonemas o tal vez ideas, combinando así varias dimensiones del lenguaje escrito.
Recientemente se han dado a conocer investigaciones muy interesantes respecto a la variación cultural (Chua y colaboradores, 2005), que puede ser incluso genética, de la percepción visual. En particular, los norteamericanos de origen europeo tienden a poner más atención visual en los objetos del plano principal, mientras que los asiáticos perciben las imágenes sin eliminar por completo los objetos secundarios. Esto podría estar relacionado con la manera en la cual las civilizaciones humanas desarrollan escrituras. Tal vez los incas tenían una habilidad de percepción global de las características de los quipus que les permitía leer con bastante velocidad sus "libros".
Epílogo
Siete de los 21 quipus hallados en Puruchuco guardan una curiosa relación entre sí. La relación entre estos quipus podría representar evidencia del desplazamiento vertical de información en la estructura administrativa del imperio inca. Existen varios pares (o parejas) de quipus que poseen secuencias numéricas iguales o muy cercanamente afines. Ocasionalmente, algunos quipus completos parecen haber sido duplicados y, con mayor frecuencia, una parte de un quipu reproduce o es correlativa con un segmento dado de otro quipu. Un quipu procedente de Chachapoyas, particularmente amplio y grande, el cual se cree representa un calendario, incorpora información igualmente contenida en otros dos quipus menores procedentes de Leymebamba.
El "Proyecto de base de datos de khipu" se inició en 2002, y tiene como meta la recolección de toda la información conocida respecto a los quipus para integrarla en un sitio centralizado. Poseer los datos e información en forma digital permite a los investigadores formular preguntas acerca de los quipus que hasta ahora hubieran sido extremadamente difíciles, si no imposibles, de responder. El Proyecto de base de datos de khipu fue financiado durante el periodo 2002-2004 por la National Science Foundation estadounidense y la Universidad de Harvard, y en 2005 es financiado por la National Science Foundation, también estadounidense.
Bibliografía
Arellano, C. (1999), "Quipu y Tocapu: Sistemas de comunicación Inca", en Los incas: arte y símbolos, F. Pease y colaboradores (editores), pp. 215-262, Lima, Banco de Crédito del Perú.
Chua, H. F., J. E. Boland, y R .E. Nisbett (2005), "Cultural variation in eye movements during scene perception", Proc. Nat. Ac. Sci.102: 12629-12633.
Domenici, V. y D. Domenici (1996), "Talking knots of the inka", Archaeology 49(6): 50-56.
Fossa, L. (2005),"Los khipu: el estado de la cuestión", diario El Peruano, sección "Identidades", 7 de nov. de 2005 (para obtener el archivo en formato PDF, contactar a los auto res).
Mann, C. C. (2003),"Cracking the khipu code", Science, 300: 1650-1651.
Silverman, G. (1994), El tejido andino: un libro de sabiduría, México, Fondo de Cultura Económica.
Urton, G. (2003), Signs of the Inka Khipu: Binary Coding in the Andean Knotted-String, Austin TX, The University of Texas Press. Urton, G. y C. J. Brezine (2005), "Khipu accounting in ancient Peru", Science, 309: 1065-1067.
Urton, G. y C. J. Brezine (2003-2004),"Proyecto de base de datos de khipu", accesible en internet (http://khipuka-mayuq.fas.harvard.edu/espanol/KG_Peabody_sp.html).
Hugo Cabrera Ibarra es matemático de la Universidad Autónoma de San Luis Potosí. Obtuvo la maestría y el doctorado en ciencias con especialidad en matemáticas básicas en el Centro de Investigación en Matematicas (cimat), de Guanajuato, y se incorporó como investigador de la División de Matemáticas Aplicadas y Sistemas Computacionales del Instituto Potosino de Investigación Científica y Tecnológica (IPICyT). Sus líneas de investigación son la teoría de nudos, los modelos topológicos y las aplicaciones de la topología a la teoría de la estabilización y a la enzimología. Es miembro del Sistema Nacional de Investigadores. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Haret C. Rosu Barbus es investigador del IPICyT, en la División de Materiales Avanzados para la Tecnología Moderna. Fue profesor investigador en el Instituto de Física de la Universidad de Guanajuato, y anteriormente trabajó en el Instituto de Física Atómica en Bucarest, Rumania. Es miembro del Sistema Nacional de Investigadores. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Luís Adolfo Torres González nació en México D.F. Fue profesor titular de la Universidad Iberoamericana en León, Guanajuato. Actualmente es estudiante de doctorado en la División de Matemáticas Aplicadas y Sistemas Computacionales del IPICyT. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Juan Pablo Treviño Gutiérrez es estudiante de maestría en la División de Matemáticas Aplicadas y Sistemas Computacionales del IPICyT. Realizó estudios de licenciatura en la Universidad de Las Américas-Puebla, con una tesis acerca de los efectos de autoimagen en fibras ópticas. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.

